要求
最近在刷算法,遇到一个有意思的题,要求如下:
设计一个数据结构,可随时插入节点,且随时查询节点集合的中位数,要求插入节点的时间复杂度为 O(logN),查询中位数的时间复杂度为 O(1)。
中位数定义:节点个数为奇数个时,为有序情况下集合的中间节点;偶数时,为中间两节点的平均值。
分析
求中位数,直觉的做法是先排序,然后根据数组的长度算出中位数,根据算法不同时间复杂度从 O(n) ~ O(NlogN) 不等。但这只适用于元素数目不变的情况,对可动态添加节点的情况,需要做到:
- 在插入时便进行重排序,时间复杂度为 O(logN)
- 不论节点个数奇偶,查中位数时间复杂度都为 O(1)
对于 第1点,二叉堆 是一个不错的选择,它拥有如下性质:
- 父节点的键值总是保持固定的序关系于任何一个子节点的键值,且每个节点的左子树和右子树都是一个二叉堆。
- 插入节点时间复杂度为 O(logN)
- 获取根结点时间复杂度为 O(1)
- 以数组形式存储结点,如果下标基于0,则:
- 结点 i 的子结点位置为 i*2 + 1与 i*2 + 2
- 反推可知,结点 i 的父节点位置为 (i – 1) / 2。
对于 第2点,可构造两个二叉堆,就可以 O(1) 复杂度查出中位数:
一个最大堆
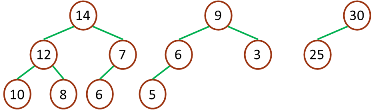
一个最小堆
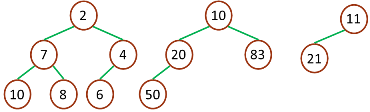
最大堆存放所有比中位数小的节点,最小堆存放所有比中位数大的节点,插入节点时动态平衡这两个二叉堆,以保证中位数总是出自这两个堆的根结点(或其一)。
思路
- 实现基础数据结构堆(Heap),提供如下功能:
- 以数组形式存储结点;
- 构造时传入 less 方法,以确定堆的性质:父和子谁大(最大/最小堆?);
- 提供 Len 方法:查询结点个数;
- 提供 Peak 方法:查询根结点;
- 提供 Insert 方法:在数组尾端插入结点,然后自下而上调整子结点与父结点:使用传入的 less 方法比较子结点,当 less(parent, child) 不为真时,进行交换——这一操作时间复杂度为 O(logN);
- 提供 Remove 方法:删除并返回根结点,然后自上而下调整父节点与它的子节点;
- 以上任一操作结束后,堆性质不变,即根结点永远是最接近中位数的。
- 基于堆实现构造数据结构 DynamicMedian,包含最大堆和最小堆,提供如下功能:
- 提供 Len 方法:查询最大最小堆中所有的结点个数;
- 提供 Median 方法:查询中位数,且:
- 结点个数为偶数时,为中间两节点的平均值;
- 结点个数为奇数时,最大堆数目多,则中位数为最大堆根结点;
- 结点个数为奇数时,最小堆数目多,则中位数为最小堆根结点。
- 提供 Insert 方法:
- 堆都为空,插入到最小堆;
- 插入结点大于等于中位数时,插入最小堆;插入结点小于中位数时,插入最大堆——如此时结点数为偶数且两个堆结点数不一致,重新平衡大小堆
实现
算法实现使用的 go 语言,堆的实现参考了标准库 “container/heap” ,自己把轮子再造一遍只是为了加深理解,没有深意 🙂
代码结构:
|
1 2 3 4 5 6 7 8 |
├── bin │ └── main.go # 跑 main 函数的脚本 ├── heap │ ├── heap_impl.go # 堆的实现 │ └── max_min_heap.go # 动态中位数数据结构 └── heap_test ├── dynamic_median_test.go # 单元测试用例 └── heap_suite_test.go # ginkgo单元测试入口 |
堆的实现:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
package heap type Heap struct { data []int lessFunc func(*[]int, int, int) bool } func (h *Heap) push(num int) { h.data = append(h.data, num) } func (h *Heap) pop() int { old := h.data n := len(old) x := old[n-1] h.data = old[0 : n-1] return x } func (h *Heap) less(i, j int) bool { return h.lessFunc(&h.data, i, j) } func (h *Heap) swap(i, j int) { h.data[i], h.data[j] = h.data[j], h.data[i] } func (h *Heap) up(j int) { for { i := (j - 1) / 2 if i == j || !h.less(j, i) { break } h.swap(i, j) j = i } } func (h *Heap) down(i, n int) { for { j1 := i*2 + 1 // left child if j1 >= n || j1 < 0 { break } j := j1 if j2 := j1 + 1; j2 < n && h.less(j2, j1) { j = j2 // right child } if !h.less(j, i) { break } h.swap(i, j) i = j } } func (h *Heap) Len() int { return len(h.data) } func (h *Heap) Peak() int { n := 0 if h.Len() > 0 { n = h.data[0] } return n } func (h *Heap) Insert(num int) { h.push(num) h.up(h.Len() - 1) } func (h *Heap) Remove() int { n := h.Len() - 1 h.swap(0, n) h.down(0, n) return (*h).pop() } |
动态中位数:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
package heap_test import ( . "../heap" . "github.com/onsi/ginkgo" . "github.com/onsi/gomega" ) var _ = Describe("validate correctness of dynamic-median algorithm", func() { It("case #1", func() { array := []int{12, 100, 16, 4, 8, 70, 2, 36, 22, 5, 46, 56, 112, 233, 666} dm := Init(&array) expected := 36 actual := dm.Median() Expect(expected).To(Equal(actual)) }) It("case #2", func() { array := []int{12, 100, 16, 4, 8, 70, 2, 36, 22, 5, 46, 56, 112} dm := Init(&array) expected := 22 actual := dm.Median() Expect(expected).To(Equal(actual)) }) }) |
单元测试:
ginkgo 是从 codewars 借鉴来的,BDD 风格很合胃口就用了,具体用法请参考官网,这里只放用例:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
package heap_test import ( . "../heap" . "github.com/onsi/ginkgo" . "github.com/onsi/gomega" ) var _ = Describe("correctness of dynamic median algorithm", func() { It("case #1", func() { array := []int{12, 100, 16, 4, 8, 70, 2, 36, 22, 5, 46, 56, 112, 233, 666} dm := Init(&array) expected := 36 actual := dm.Median() Expect(expected).To(Equal(actual)) }) It("case #2", func() { array := []int{12, 100, 16, 4, 8, 70, 2, 36, 22, 5, 46, 56, 112} dm := Init(&array) expected := 22 actual := dm.Median() Expect(expected).To(Equal(actual)) }) }) |
在 heap_test 目录下运行 ginkgo 命令,将得到校验结果 :
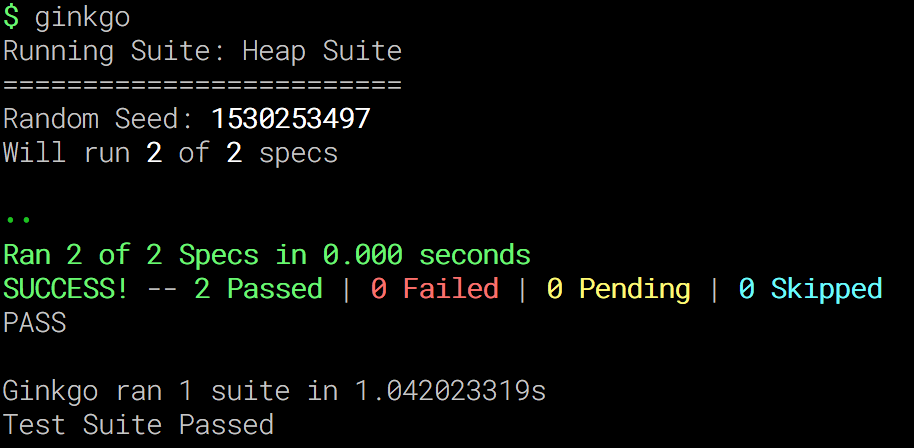
引用
- https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E5%A0%86
- http://bubkoo.com/2014/01/14/sort-algorithm/heap-sort/
- https://stackoverflow.com/questions/15319561/how-to-implement-a-median-heap
打赏作者
您的支持将激励我继续创作!


Leave a Reply for darkhorse Cancel Reply